|
En 1854 George
Boole introdujo una notación simbólica para el tratamiento de
variables cuyo valor podría ser verdadero o falso (variables
binarias) Así el álgebra de Boole nos permite manipular
relaciones proposicionales y cantidades binarias. Aplicada a
las técnicas digitales se utiliza para la descripción y diseño
de circuitos mas económicos. Las expresiones booleanas serán
una representación de la función que realiza un circuito
digital. En estas expresiones booleanas se utilizarán las tres
operaciones básicas ( AND, OR NOT ) para construir expresiones
matemáticas en las cuales estos operadores manejan variables
booleanas (lo que quiere decir variables binarias).
Elementos
del álgebra de Boole
No es objeto de este curso
un análisis profundo y formal de los postulados y teoremas del
Algebra de Boole.
Los símbolos elementales
son:
· 0: representativo de
FALSO
· 1: representativo de
VERDADERO
Las operaciones
fundamentales son:
· Conjunción
u operación AND (se representa con
·
)
· Disyunción u operación OR
(se representa con + )
·
Complementación, Negación u operación NOT ( se representa con
una barra sobre la variable,  )
)
Las variables son las
proposiciones, que se representan o simbolizan por
letras
Postulados:
Los postulados para las tres
operaciones básicas, AND, OR Y NOT, son suficientes para
deducir cualquier relación bolean.
| OR |
AND |
NOT |
0 + 0 = 0
0 + 1 = 1
1 + 0 = 1
1 + 1
= 1 |
0 · 0 =
0
0 · 1 = 0
1 ·
0 = 0
1 · 1 = 1 |

 |
Teoremas:
1. Regla del cero y la unidad
a) X + 0 = X
b) X + 1 = 1 |
c) X
· 1 = X
d) X
· 0 =
0 | |
2. Idempotencia o potencias
iguales
| a) X + X = X
|
b) X
· X =
X | |
3. Complementación
a) X + 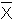 = 1 = 1 |
b) X · 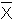 =
0 =
0 | |
5. Conmutatividad
a) conmutatividad del +
X + Y = Y +
X |
b) conmutatividad del
·
X ·
Y = Y · X
| |
| 