|
Ingº Nelson Carranza
Medina
CIRCUITOS DIGITALES COMBINACIONALES
COMPUERTAS LÓGICAS
CIRCUITOS COMBINACIONALES
Los circuitos combinacionales generan un estado en sus salidas
que es una combinación lógica de las entradas presentes
en ese momento, en el momento que cambie la entrada, la salida cambia
al correspondiente estado de salida.
Se describen en esta lección los circuitos combinacionales
más usados con referencias a los circuitos integrados correspondientes
y ejemplos de aplicación.
COMPUERTAS LOGICAS
Son circuitos que generan voltajes de salida en función
de la combinación de entrada correspondientes a las Funciones
Lógicas, en este curso se usa la analogía llamada
lógica positiva en la cual alto (H)
corresponde a Verdadero y bajo (L)
corresponde a Falso.
COMPUERTA AND DE 2 ENTRADAS
Símbolo y diagrama de pines del 7408 integrado de 4 compuertas
AND de 2 entradas en la tecnología TTL. En CMOS es el 4081
pero tiene una distribución de pines diferente (consultar
el manual).
Ejemplo de funcionamiento y Tabla de verdad
La función lógica que representa la compuerta es:
F=A·B y se lee "F igual a A and B".
COMPUERTA AND DE 3 ENTRADAS
Símbolo y diagrama de pines del 7411 integrado de 4 compuertas
AND de 2 entradas en la tecnología TTL. En CMOS es el 4073
pero tiene una distribución de pines diferente (consultar
el manual).
Ejemplo de funcionamiento y Tabla de verdad
La función lógica que representa la compuerta es:
F=A·B·C y se lee "F igual a A and B and C".
En la practica de los electrónicos se acostumbra usar la
analogía L = 0 (se dice cero lógico) y H = 1 (uno
lógico), entonces es común usar las tablas así:
| A and B |
|
A and B and C |
| B |
A |
F |
| 0 |
0 |
0 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
1 |
|
|
| C |
B |
A |
F |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
| 1 |
1 |
1 |
1 |
|
OTRAS FUNCIONES LOGICAS
En forma similar presentamos las compuertas lógicas que
representan a las demás Funciones Lógicas.
COMPUERTA OR
| A or B |
|
A or B or C |
| B |
A |
F |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
|
|
| C |
B |
A |
F |
| 0 |
0 |
0 |
0 |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
1 |
|
En TTL: 7432 En
TTL: 74
En CMOS: 40 En
CMOS: 40
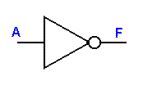
COMPUERTA INVERSOR
 (A negado)
En TTL: 7404, En CMOS: 40
COMPUERTA NOR
| A nor B |
|
A nor B nor C |
| B |
A |
F |
| 0 |
0 |
1 |
| 0 |
1 |
0 |
| 1 |
0 |
0 |
| 1 |
1 |
0 |
|
|
| C |
B |
A |
F |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
0 |
| 0 |
1 |
0 |
0 |
| 0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
0 |
| 1 |
0 |
1 |
0 |
| 1 |
1 |
0 |
0 |
| 1 |
1 |
1 |
0 |
|
En TTL: 7402 En
TTL: 74
En CMOS: 40 En
CMOS: 40
COMPUERTA NAND
| A nand B |
|
A nand B nand C |
| B |
A |
F |
| 0 |
0 |
1 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
|
|
| C |
B |
A |
F |
| 0 |
0 |
0 |
1 |
| 0 |
0 |
1 |
1 |
| 0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
1 |
| 1 |
0 |
0 |
1 |
| 1 |
0 |
1 |
1 |
| 1 |
1 |
0 |
1 |
| 1 |
1 |
1 |
0 |
|
En TTL: 7400 En
TTL: 74
En CMOS: 40 En
CMOS: 40
COMPUERTA EXOR
| B |
A |
F |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
0 |
En TTL: 7486, En CMOS: 40
ANALISIS DE CIRCUITOS COMBINACIONALES
El análisis consiste en que dado un circuito conocer el
valor de sus salidas para cada una de las posibles combinaciones
de entrada, este resultado se representa en la Tabla de Verdad del
circuito y la función Booleana que representa el circuito.
Ejemplo
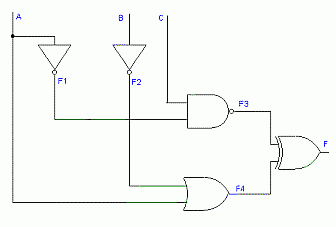 La
función Booleana se obtiene generando la correspondiente
expresión para cada compuerta y haciendo los reemplazos hasta
obtener una sola expresión que represente todo el circuito. La
función Booleana se obtiene generando la correspondiente
expresión para cada compuerta y haciendo los reemplazos hasta
obtener una sola expresión que represente todo el circuito.
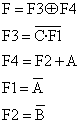
Reemplazando: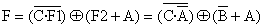
La tabla de Verdad se forma con la lista de combinaciones según
el número de variables de entrada (ver Funciones Lógicas)
y una columna por cada salida del circuito, con cada combinación
de entrada se van hallando los valores de salida de cada compuerta
usando las tablas de verdad de cada función básica
hasta calcular el valor de la salida del circuito y se va colocando
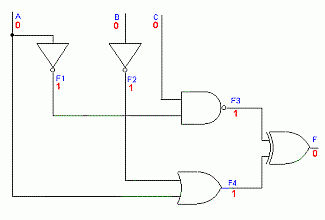
el correspondiente valor en la tabla, en la gráfica siguiente
se ven los valores para la combinación de entrada A=0 B=0
C=0:
F1=(0 negado)=1 F2=(0 negado)=1 F3=(0 nand 1)=1 F4=(1 or 0)=1
F=(1 exor 1)=0
| C |
B |
A |
F1 |
F2 |
F3 |
F4 |
F |
| 0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
| 0 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
| 0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
| 0 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
| 1 |
0 |
1 |
0 |
1 |
1 |
1 |
0 |
| 1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
| 1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
|