|
Simplificación de funciones con mapas
de Karnaugh
Obtener la función de
un Mapa de Karnaugh es el procedimiento inverso a la de
la realización del mapa. Un termino de la función coloca
uno o mas "unos" en el mapa de Karnaugh.
Tomar esos
unos, agrupándolos de la forma adecuada, nos permite
obtener los términos de la función
Utilizaremos los Mapas
de Karnaugh para obtener una función mínima de dos
niveles Suma de Productos.
Una expresión de dos
niveles sdp se considerará la expresión mínima si:
1.
No existe otra expresión equivalente que incluya menos
productos.
2. No hay otra expresión equivalente que
conste con el mismo numero de productos, pero con un
menor numero de literales.
Observe que hablamos
de UNA expresión mínima y lo LA expresión mínima. Esto
porque pueden existir varias expresiones distintas, pero
equivalentes, que satisfagan esta definición y tengan el
mismo numero de productos y literales.
La minimización de
funciones sobre el mapa de Karnaugh se aprovecha del
hecho de que las casillas del mapa están arregladas de
tal forma que entre una casilla y otra, en forma
horizontal o vertical existe ADYACENCIA LOGICA. Esto
quiere decir que entre una casilla y otra solo cambia
una variable.
Definimos los mintérminos adyacentes
desde el punto de vista lógico como dos mintérminos que
difieren solo en una variable. Agrupando casillas
adyacentes obtenemos términos productos que eliminan las
variables que se complementan, resultando esto en una
versión simplificada de la expresión.
El procedimiento es el
de agrupar "unos" adyacentes en el mapa; cada grupo
corresponderá a un termino producto, y la expresión
final dará un OR (suma) de todos los términos producto.
Se busca obtener el menor numero de términos productos
posible, lo que implica que cada termino producto debe
contener el mayor numero de mintérminos
posibles.
|
Antes de
comenzar formalmente con la discusión sobre
minimización veamos por un momento el
siguiente mapa de Karnaugh, resultado de la
función: |
|
|
_ |
_ |
_ |
_ |
|
_ |
|
_ |
_ |
|
|
|
_ |
_ |
|
|
_ |
_ |
_ |
|
_ |
|
_ |
|
|
|
|
_ |
|
|
|
_ |
_ |
|
|
|
|
|
|
|
|
_ |
|
|
|
_ |
_ |
|
_ |
|
_ |
|
|
_ |
|
|
|
|
_ |
|
|
_ |
|
_ |
| f |
= |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
|
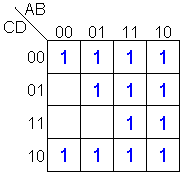
Como podemos
notar, la función está expresada en forma
canónica, por lo que cada mintérmino "colocará" un
1 en su casilla correspondiente como se muestra en
el mapa de Karnaugh correspondiente. |
 |
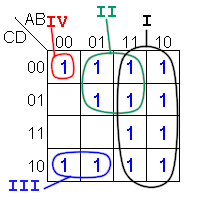 |
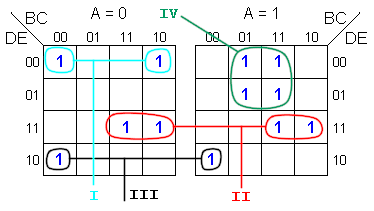
Supongamos por
un momento que agrupemos los "unos" del mapa de
Karnaugh como se muestra en la figura.
Según
esto tenemos cuatro términos que son:
|
|
|
|
|
|
| termino
I |
A |
|
|
|
(agrupa
8 unos y es de 1 variable) |
|
|
_ |
|
|
|
| termino II
|
B |
C |
|
|
(agrupa
4 unos y es de 2 variables) |
|
_ |
|
_ |
|
|
| termino III |
A |
C |
D |
|
(agrupa
2 unos y es de 3 variables) |
|
_ |
_ |
_ |
_ |
|
| termino IV |
A |
B |
C |
D |
(agrupa
1 uno y es de 4
variables) | |
Puede verse que a
medida que agrupamos mayor cantidad de "unos", el
termino tiene menos literales. El agrupamiento se hace
con una cantidad de "unos" que son potencias de 2. Así
agrupamos 2 mintérminos, 4 mintérminos y 8 mintérminos.
Cada vez que aumentamos, el termino va eliminando una
variable. En una función de 4 variables, un termino que
tenga un solo "uno" tendrá las cuatro variables. De
hecho es un termino canónico. Al agrupar dos mintérminos
eliminaremos una variable y el termino quedará de
tres variables. Si agrupamos cuatro "unos" eliminaremos
dos variable quedando un termino de dos variables y
finalmente si agrupamos ocho "unos" se eliminaran tres
variable para quedar un termino de una variable.
Todo
esto se debe a la adyacencia entre casillas y cada vez
que agrupamos, se eliminan las variables que se
complementan.
En el
ejemplo anterior la función obtenida es:
|
|
|
_ |
_ |
_ |
_ |
|
_ |
|
_ |
|
|
_ |
|
|
|
f |
= |
A |
B |
C |
D |
+ |
A |
C |
D |
+ |
B |
C |
+ |
A |
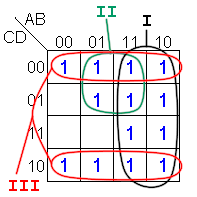
| Pero, ¿será
esta la función mínima?
Si vemos la figura a la
derecha, la forma de agrupar nos da como
resultado: |
|
|
_ |
|
|
_ |
|
|
|
| f |
= |
D |
+ |
B |
C |
+ |
A |
que sí es
expresión
mínima. |
Es importante
que al "tomar" un uno, se agrupe con todos los
unos adyacentes, aunque estos uno sean parte de
otros grupos. Fíjese que el mintérmino 13
(11002) es común
a los tres términos. |
 |
Para simplificar
funciones utilizando mapas de Karnaugh hay que tener en
cuenta que:
-
Cada casilla
(mintérmino) en un mapa de Karnaugh de n variable
tiene n casillas adyacentes lógicamente, de modo que
cada par de casillas defiere en una
variable
-
Al combinar las
casillas en un mapa de Karnaugh, agruparemos un número
de mintérminos que sea potencia de dos. Así agrupar
dos casillas eliminamos una variable, al agrupar
cuatro casillas eliminamos dos variables, y así
sucesivamente. En general, al agrupar 2n casillas eliminamos n
variables.
-
Debemos agrupar
tantas casillas como sea posible; cuanto mayor sea el
grupo, el termino producto resultante tendrá menos
literales. Es importante incluir todos los "unos"
adyacentes a un mintérmino que sea igual a
uno.
-
Para que hayan menos
términos en la función simplificada, debemos formar el
menor numero de grupos posibles que cubran todas las
casillas(mintérminos) que sean iguales a uno. Un
"uno" puede ser utilizado por varios grupos, no
importa si los grupos se solapan. Lo importante es que
si un grupo está incluido completamente en otro grupo,
o sus "unos" están cubiertos por otros grupos, no hace
falta incluirlo como termino.
Terminología para la simplificación:
Implicante, Implicante Primo, Implicante Primo
Esencial.
A continuación
definiremos algunos términos comúnmente utilizados en
los procesos de simplificación de funciones
lógicas.
Implicante:
Conjunto de unos en
un mapa de Karnaugh que representa un termino producto
de variables. Se denomina implicante porque cuando este
termino toma el valor 1, implica que también la
función toma el valor 1. Un mintérmino solo es un
implicante.
Implicante Primo:
Implicante que no está
incluido completamente dentro de otro implicante. No
puede combinarse con otro implicante para eliminar un
literal.
Implicante Primo Esencial:
Implicante primo que
contiene uno o mas mintérminos que no están incluidos en
cualquier otro implicante primo.
|
|
|
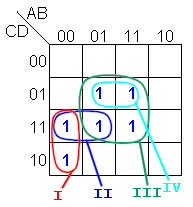
En el siguiente mapa de
Karnaugh:
Los términos I II y III
son implicantes primos
El termino IV no es implicante
primo
Los términos I y III son
implicantes primos esenciales
El termino II no es un
implicante primo esenciales
La función se obtiene con los
términos I y III |
Algoritmo de minimización mediante mapas
de Karnaugh
1. Identificar los
implicantes primos. Para esto se busca obtener los
grupos con mayor cantidad de unos adyacentes. Los grupos
deben contener un numero de unos que son potencias de
2.
2.Identificar
todos los implicantes primos esenciales
3.La expresión mínima
se obtiene seleccionando todos los implicantes primos
esenciales y el menor numero de implicantes primos para
cubrir los mintérminos no incluidos en los implicantes
primos esenciales.
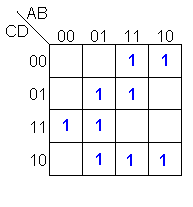
Ejemplo: Simplificar la
función:
|
|
_ |
_ |
|
|
|
_ |
|
_ |
|
|
_ |
|
|
_ |
|
_ |
|
|
|
|
|
_ |
_ |
_ |
|
|
_ |
|
_ |
|
|
|
_ |
_ |
|
|
|
_ |
|
|
|
|
|
_ |
| f |
= |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
+ |
A |
B |
C |
D |
En los mapas siguientes se
muestra el proceso de simplificación utilizando el
algoritmo. |
|
|

|
|
|
|
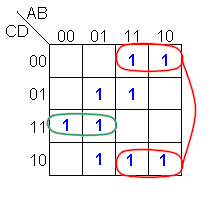
Implicantes
primos |
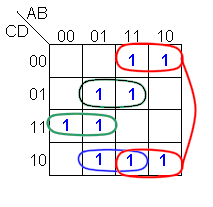
Implicantes
primos esenciales |
|
|
|
_ |
|
|
|
_ |
|
_ |
|
|
|
|
|
_ |
|
F(A,B,C,D) |
= |
B |
C |
D |
+ |
A |
D |
+ |
A |
C |
D |
+ |
B |
C |
D | |
|
Para practicar
puede bajar esta programa freeware muy
intuitivo y fácil de usar. Llenas la tabla de
verdad y a medida que vas colocando los unos, se
va llenando el mapa de Karnaugh y se van
agrupando los términos. También se pueden marcar
los unos directamente en el mapa de Karnaugh. No
se requiere instalación. Ocupa 283 Kb. Haz click
en el icono para bajarlo. |

|
Los ejemplos
anteriores se realizaron con funciones de 4 variables.
Para mapas de Karnaugh de 5 y 6 variables el
procedimiento es esencialmente el mismo solo hay que
recordar que un mintermino es adyacente a otro
mintermino que ocupe la misma posición en forma
horizontal o vertical en los cuadrados a los lados del
mapa.
Minimización en mapas de Karnaugh de
5 variables
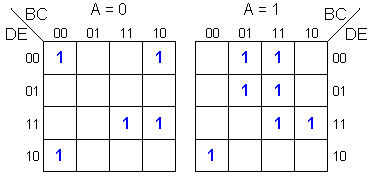
Simplificar la función
=  m(0,2,8,11,15,18,20,21,27,28,29,31) m(0,2,8,11,15,18,20,21,27,28,29,31)
|
Se coloca un 1 en
los minterminos
 |
|
|
|
_ |
_ |
_ |
_ |
|
|
|
|
|
_ |
_ |
|
_ |
|
|
|
_ |
|
La función
quedará f |
= |
A |
C |
D |
E |
+ |
B |
D |
E |
+ |
B |
C |
D |
E |
+ |
A |
C |
D | |
Minimización en mapas de Karnaugh de
6 variables
Obtenga una función
mínima para el siguiente mapa de Karnaugh
 |
pinche aquí para
ver la solución 
| | 