|
Sistemas de numeración
| Se
entiende por base de sistema de numeración el número
de dígitos necesarios para cambiar de una unidad a
otra inmediatamente inferior o superior entendiendo por cada
simbolo un dígito (bit).
Para
transformar un número decimal a binario se va dividiendo
por 2 y se van escribiendo los residuos, luego se leen estos
de abajo hacia arriba y asi se obtiene el número binario
pedido. |
Ejemplo
# 1:
| # |
|
D |
|
|
residuo |
binario |
| 15 |
/ |
2 |
= |
7 |
si |
1 |
| 7 |
/ |
2 |
= |
3 |
si |
1 |
| 3 |
/ |
2 |
= |
1 |
si |
1 |
| 1 |
/ |
2 |
= |
0 |
si |
1 |
El
número 15 en binario es 1111
Ejemplo
# 2:
| # |
|
D |
|
|
residuo |
binario |
| 40 |
/ |
2 |
= |
20 |
no |
0 |
| 20 |
/ |
2 |
= |
10 |
no |
0 |
| 10 |
/ |
2 |
= |
5 |
no |
0 |
| 5 |
/ |
2 |
= |
2 |
si |
1 |
| 2 |
/ |
2 |
= |
1 |
no |
0 |
| 1 |
/ |
2 |
= |
0 |
si |
1 |
El
número 40en binario es 101000
Ejemplo
# 3:
| # |
|
D |
|
|
residuo |
binario |
| 262 |
/ |
2 |
= |
131 |
no |
0 |
| 131 |
/ |
2 |
= |
65 |
si |
1 |
| 65 |
/ |
2 |
= |
32 |
si |
1 |
| 32 |
/ |
2 |
= |
16 |
no |
0 |
| 16 |
/ |
2 |
= |
8 |
no |
0 |
| 8 |
/ |
2 |
= |
4 |
no |
0 |
| 4 |
/ |
2 |
= |
2 |
no |
0 |
| 2 |
/ |
2 |
= |
1 |
no |
0 |
| 1 |
/ |
2 |
= |
0 |
si |
1 |
El
número 262 en binario es 100000110
Ejemplo
# 4:
| # |
|
D |
|
|
residuo |
binario |
| 233 |
/ |
2 |
= |
116 |
si |
1 |
| 116 |
/ |
2 |
= |
58 |
no |
0 |
| 58 |
/ |
2 |
= |
29 |
no |
0 |
| 29 |
/ |
2 |
= |
14 |
si |
1 |
| 14 |
/ |
2 |
= |
7 |
no |
0 |
| 7 |
/ |
2 |
= |
3 |
si |
1 |
| 3 |
/ |
2 |
= |
1 |
si |
1 |
| 1 |
/ |
2 |
= |
0 |
si |
1 |
El
número 233 en binario es 11101001
| Lea
detenidamente los postulados se que dan a continuación
para que pueda entender bien el comportamiento de los circuitos
digitales. |
| Postulados
y Teoremas del algebra de Boole |
Postulado
# 1:
La
suma lógica de dos o más variables equivale a la realización
práctica de contáctos en paralelo.
A
+ B = S
Tabla
de la verdad:
| A |
B |
Salida |
| 0 |
0 |
0 |
| 0 |
1 |
1 |
| 1 |
0 |
1 |
| 1 |
1 |
1 |
| (Circuito
"OR")
Para
la construcción de la tabla de la verdad es necesario
conocer el número de combinaciones posibles de las
variables, éste número es igual a la base 2
a la "n", donde "n" representa el número
de variables. |
Compuerta
OR:
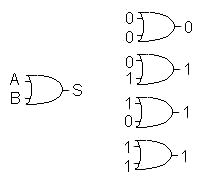
Postulado
# 2:
A
x B = S
El
producto lógico de dos o más variables equivale a
la realización práctica de circuitos serie (contáctos
en serie).
Compuerta
"AND"
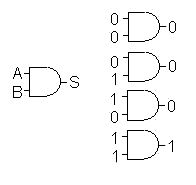
Postulado
# 3:
A
+ 1 = 1
La
asociación eléctrica en paralelo de un contácto
A con otro siempre cerrado es igual a uno (1).
Postulado
# 4:
A
+ 0 = A
La
asociación de un contácto "A" en paralelo
con otro siempre abierto es igual a "A".
Postulado
# 5:
A
x 1= A
Postulado
# 6:
A
x 0 = 0
Un
contácto "A" en serie con otro siempre abierto
es igual a cero.
Postulado
# 7:
A
+ A = A
Un
contácto "A" en paralelo con otro contácto
de su misma denominación igual al contácto "A".
Postulado
# 8:
A
x A = A
Dos
contáctos iguales en serie equivalen a un sólo contácto
"A".
Postulado
# 9:
Esta
es la propiedad conmutativa de la suma lógica la cual nos
dice que el resultado de una distribución de contáctos
en paralelo es independiente de su disposición.
A
+ B = B + A
Postulado
# 10:
Postulado
# 11:
| En
el algebra de Boole deben utilizarce paréntesis, corchetes,
llaves, etc., para indicar el orden de las operaciones del circuito
lógico. |
A
x B x C = (A x B) x C = B x (A x C)
Postulado
# 12:
| Propiedad
distributiva del producto lógico la cual nos dice que
la asociación en serie de un contácto con otros
dos en paralelo equivalen a la asociación en paralelo
de dos circuitos series formados por el producto en paralelo
con cada uno de los otros dos. |
A
x (B + C) = (A x B) + (A x C)
Postulado
# 13:
A
+ (B x C) = (A + B) x (A + C)
Postulado
# 14:
| Antes
de poner en evidencia este postulado debemos aclarar que entenderemos
por negación de una variable a ella misma afectada por
el signo de negación, asi " A´ " se lee
como negación de "A" o "A" negada. |
Si
A = 1 entonces A´ = 0
Si
A = 0 entonces A´ = 1
Una
variable en paralelo con su inverso siempre es igual a uno (1).
A
+ A´ = 1
Postulado
# 15:
Una
variable "A" en serie con su inversa siempre es cero.
A
x A´ = 0
Postulado
# 16:
| Este
postulado nos muestra como dando un doble inversión a
una variable cualquiera o a una función cualquiera ésta
no varía. |
A´´
= A
Postulado
# 17:
Si
invertimos los miembros de una igualdad ésta no varía.
A
+ B = S
(A
+ B)´ = S´
|
Teorema # 1: (Absorción)
A
+ A´. B = A
A
. (1 + B) =
A
. 1 = A |
Teorema
# 2: (Absorción)
A
. (A + B) = A
(A
. A) + (A . B) =
A
+ A . B = A
A
. (1 + B) = A . 1 = A
|
|
Teorema
# 3:
A
+ (A´ . B) = A + B
(A
+ A´) . (A + B) =
1
. (A + B) = A + B
|
Teorema
# 4:
(A
+ B´) . B = (A . B)
(A
. B) + (B . B´) =
A
. B + 0 = A . B |
|
Teorema
# 5:
(A
+ B) . (A´+ C) = A . C + A´. B
|
Teorema
# 6:
(A
+ B )´ = A´. B´
|
|
Teorema
# 7:
(A
. B)´= A´ + B´
|
|
| SIMPLIFICACION
DE FUNCIONES |
| Con
la ayuda de los postulados y teoremas vistos resulta evidente
que ciertas funciones podrán ser simplificadas dando
como resultado otras funciones equivalentes más sencillas,
cuya realización electiva mediante contáctos o
mediante funciones "OR" y funciones "AND"
podran llevarse a cabo de una manera más simple y económica. |
Ejemplo
#1:
S
= A´.B + A.B
El
primer paso es sacar factor común "B".
S
= B.(A´ + A)
Según
el postulado # 14, (A´+ A) = 1
S
= B.1
S
= B
Ejemplo
#2:
S
= A.B.C + A´.B.C + A.B´.C
S
= A.C.(B + B´) + A´.B.C
S
= A.C + A´.B.C
S
= C.(A + A´.B) ; Aplicando el teorema #1 nos queda:
S
= C.(A + B)
Ejemplo
#3:
S
= A.B + A.C + A.D.A + A.A´.B´ + A.C.D + A.A´.B´.C
S
= A.B + A.C + A.D.A + A.C.D
S
= A . (B + C + D + C.D)
S
= A . (B + C + D)
Obtención
de expresiones algebraicas correspondientes a circuitos
dados.
Para
obtener la expresión algebraica de un circuito se
van siguiendo los diferentes caminos en serie desde la entrada
hasta la salida para luego agrupar estos caminos en paralelo.
Es conveniente recordar siempre éste método,
aunque la práctica nos dará la ecuación
con sólo observar el diagrama.
|
Ejemplo
#1:
Obtenga
la expresión algebraica del siguente circuito:
S
= A . B + C . D + F
Ejemplo
#2:
Obtenga
la expresión algebraica del siguente circuito:
S
= A . B . (C . D + e´.F) . G
Ejemplo
#3:
Obtenga
la expresión algebraica del siguente circuito:
S
= A.B´ + A´.B
Ejemplo
#4:
Obtenga
la expresión algebráica del siguente circuito:
S1
= (A + B) . C
S2
= A . (B.C.E + D)
Ingº Nelson
Carranza Medina |