|
Los mapas de Karnaugh
constituyen un método sencillo y apropiado para la
minimización de funciones lógicas. El tamaño del mapa depende
depende del numero de variables, y el método de minimización
es efectivo para expresiones de hasta 6 variables.
Representación de funciones con mapas de
Karnaugh
Un mapa de Karnaugh
es una representación gráfica de una tabla de verdad, y por lo
tanto existe una asociación unívoca entre ambas. La tabla de
verdad tiene una fila por cada mintérmino, mientras que el
mapa de Karnaugh tiene una celda por cada mintérmino. De
manera análoga, también existe una correspondencia unívoca
entre las filas de la tabla de verdad y las celdas del mapa de
Karnaugh si se utilizan maxtérminos.
El proceso de
minimización usando como herramienta los mapas de Karnaugh se
basa en la forma en como se acomodan las celdas del mapa que
representan cada una un mintérmino.
|
Al igual que en una
tabla de verdad, en la que colocamos 1 o 0 en el valor
de la función correspondiente a una de las 2n combinaciones, así hacemos en un mapa de
Karnaugh, colocando un 1 en la celda correspondiente a
la combinación para la cual la función vale 1 y dejando
en blanco las celda correspondientes a la combinación
para la cual la función vale
0. |
 |
|
Para entender como se
representa un mapa de Karnaugh, supongamos que K sea el
conjunto de los ceros y unos de una función y su
representación sea un rectángulo o un cuadrado, Como se
muestra en la figura. |
 |
|
Una variable A podrá
asumir sólo dos valores de verdad: 0 o 1, por lo que
podemos dividir K en dos porciones:
una donde A vale
cero ( A no existe)
otra donde A vale uno ( A
existe) |
 |
|
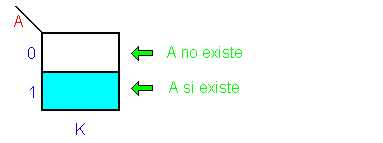Ordinariamente solo se
coloca la variable A y el 0 y 1 para indicar las áreas
de existencia de A y  .
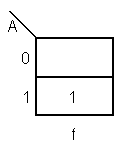
Si deseamos representar en el mapa una
función dependiente de A, solo necesitaremos indicar en
que parte se encuentra. Sea por ejemplo f = A : f existe
en el área en que A existe ( f = 1 si A = 1). Podemos
entonces señalar el área de A como la región de
existencia de f. Esto lo hacemos colocando un 1 donde f
= 1. |
 |
|
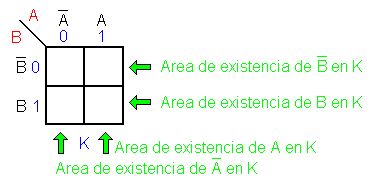
Consideremos ahora dos
variables A y B que deben tener una representación en K.
Cuatro son las formas posibles de combinar A y B:
A=0 y B=0, A=0 y
B=1, A=1 y B=0, A=1 y B=1.
Note que cada uno de
los 4 cuadrados en los que se subdivide el mapa
corresponde a un mintérmino. Por ejemplo el cuadrado
superior izquierdo corresponde a la combinación A = 0 y
B = 0. Esto es la INTERSECCION del área donde A vale 0
con el área donde B vale 0, lo que podemos expresar como
· . |
 |
Recuerde que la
combinación · en una función de 2 variables es el
mintérmino m0 .
SI TODAVIA TIENE DUDAS CON LAS
DEFINICIONES DE MINTÉRMINO Y MAXTÉRMINO REPASE LA GUIA
DE ALGEBRA
DE BOOLE |
| Mapas de Karnaugh de 2
variables |
|
Sea f una
función de 2 variables f (A,B)
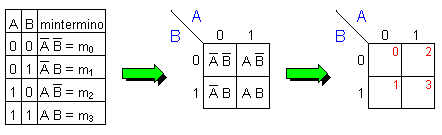
Para elaborar el
mapa de Karnaugh tendremos 22 = 4
combinaciones.
En la figura se muestra la
tabla de verdad con la lista de los mintérminos y
el lugar que ocupa cada uno de ellos en un mapa.
|
 |
|
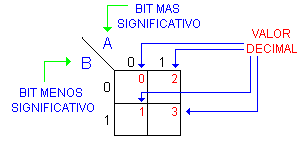
Una manera mas
sencilla de representar el mintérmino en la
casilla correspondiente es señalando su valor
decimal.
Por ejemplo
la combinación A=1 y B=1 es el termino AB cuyo
valor binario es 11 y que convertido a decimal da
3. (Mintérmino m3).
|
 |
|
| Mapas de Karnaugh de 3
variables |
|
Sea f una función de 3
variables:f (A,B,C)
Para elaborar el mapa
de Karnaugh tendremos 23 = 8
combinaciones.
Al igual que antes cada casilla del
mapa corresponde a un mintémino de la tabla de verdad.
Es importante colocar las variables en el orden
indicado de mas significativo a menos significativo (A,
B, C), de otra forma el valor decimal de las casilla
sería diferente.
|
 |
|
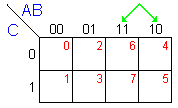
CUIDADO: Note que en
las columnas AB no se sigue el orden progresivo de
valores, 00, 01, 10, 11 sino 00, 01,11,10.
Esto
es muy importante, ya que el proceso de
minimización depende de la ubicación de las
casillas en el mdk. Esto se hace para que entre
una casilla y otra, en forma horizontal o vertical
solo cambie una variable, lo que llamamos
ADYACENCIA LOGICA.
Por ejemplo la casilla 2
(010) es adyacente a las casillas 0 (000)(cambia
B), a la 3 (011)(cambia C) y a la 6 (110)(cambia
A).
¿ Cuales son las casillas adyacentes a la
casilla 4? Note que además de la 6 y la 5 también
es adyacente a la 0 ( entre 100 (4) y 000 (0)
cambia A) |
 |
|
Antes de seguir con 4, 5 y 6
variables veamos como se representa una función en un mapa de
Karnaugh:
1.
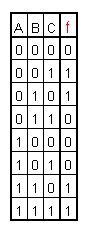
Desde la tabla de verdad
Supongamos que tenemos la
siguiente tabla de verdad para una función de 3 variables
f(ABC):
 |
|
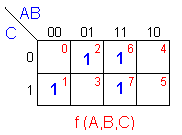
El mapa de
Karnaugh se obtiene colocando un 1 en las
casillas correspondientes a las combinaciones
para las cuales la función es igual a 1.
En este caso para
las combinaciones: |
| _ |
_ |
|
|
_ |
|
_ |
|
|
|
_ |
|
|
|
|
| A |
B |
C |
,
|
A |
B |
C |
,
|
A |
B |
C |
,
|
A |
B |
C | | |
| |
2. Directamente desde una
función.
Para este caso la función
puede ser o no canónica. Si es canónica cada termino producto
es un mintérmino, por lo que tiene una casilla especifica en
el mapa de karnaugh.
|
|
|
|
_ |
_ |
|
|
_ |
|
_ |
|
|
|
_ |
|
|
|
|
|
Por
ejemplo la función |
f |
= |
A |
B |
C |
+ |
A |
B |
C |
+ |
A |
B |
C |
+ |
A |
B |
C |
Es una función canónica
(cada termino producto posee todos los literales de la
función) y tendrá la misma representación que el mdk anterior
ya que corresponde a la función de la tabla de
verdad.
En este punto es bueno
recordar el significado geométrico de los mapas de Karnaugh.
Si tomamos una función de 3 variables, f( A,B,C), en el mdk
debemos poder representar lo siguiente el área de existencia
de A, de , de B, de , de C y de  .
Esto se realiza de la
siguiente manera:
Una casilla del mapa
corresponde a un mintérmino. Por ejemplo la casilla 6
corresponde a la combinación AB que quiere decir A=1 Y B=1 Y C=0. Esto es el AND de
A, B y .
Geométricamente se representa como la
INTERSECCION de las áreas donde A existe , B existe y existe. Si sobreponemos estas áreas, la única
casilla común es la casilla 6 y es la representación de AB
Siguiendo esta misma
relación el OR es la UNION de áreas. Pruebe como ejercicio a
representar en un mapa de Karnaugh de 2 variables la función f
= A+B y compárela con la tabla de verdad del OR.
Con lo dicho anteriormente,
cuando la función es canónica, la intersección de las áreas
que representan a los literales del termino solo coinciden en
una casilla y por eso cada mintérmino tiene su casilla
correspondiente.
¿ Que sucede cuando la
función no es canónica?
Pruebe a representar la
función f(A,B,C)= A B + B + C
Esta función no es canónica
( el primer termino no tiene todas las variables de la
función). Si utilizamos el mismo razonamiento gráfico podemos
decir que la función es la UNION de las áreas que representan
cada uno de los términos, y cada termino es la INTERSECCION de
las áreas que representan sus literales.
El termino AB será la
intersección de las áreas de A=1 y B=1, el termino B la intersección de las áreas de A=0, B=1 y
C=0 y el termino C la intersección de las áreas de A=0, B=0 y C=1 . El
mapa final se obtiene con la unión de los tres
resultados.
Si vemos este resultado es
el mismo que obtuvimos para el ejemplo anterior. Su
representación en un mapa de karnaugh es la misma por lo que
las funciones son equivalente. Esto quiere decir
que:
A B + A B C + B + C = A B + B + C
Si lo demostramos utilizando
álgebra de Boole :
AB(C+ ) + B + C = A B + B + C
AB + B + C = A B + B + C
El hecho de simplificar
AB(C+ ) = AB es lo que gráficamente llamamos
ADYACENCIA LOGICA y que nos servirá para minimizar
directamente desde el mdk sin utilizar manejo algebraico.
 Problema: Demuestre con
mapas de Karnaugh que +A + A C + A B C = AC + |
| Mapas de Karnaugh de 4
variables |
|
Sea f una función de 4
variables:f (A,B,C,D)
Para elaborar el mapa
de Karnaugh tendremos 24 = 16
combinaciones.
Siguiendo el mismo procedimiento que
para la función de 3 variables obtenemos el mapa que se
muestra en la figura.
Note el orden en que se
colocan las variables A, B,C y mas
significativo a menos significativo.
También como
antes para las columnas AB, las filas CD siguen el
orden 00, 01, 11, 00 para que haya adyacencia
lógica |
|
| Mapas de Karnaugh de 5
variables |
|
Sea f una función de 5
variables:f (A,B,C,D,E)
Para elaborar el mdk
tendremos 25 = 32
combinaciones.
Note que ahora una casilla, además de
ser adyacente en forma horizontal o vertical, es
adyacente a la casilla que ocupa la misma posición
en el cuadrado cercano.
Por ejemplo la casilla
15(01111) es adyacente al las casillas 13, 7, 14, 11 y a
la 31(1111)
Esto porque cambia una
sola variable entre una casilla y otra. |
|
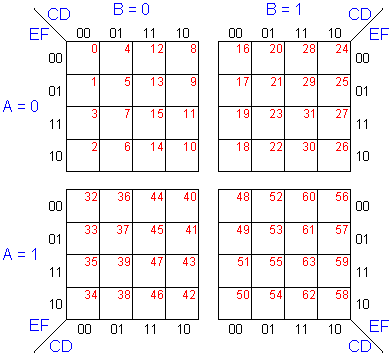
| Mapas de Karnaugh de 6
variables |
|
Sea f una función de 6
variables:f (A,B,C,D,E,F)
Para elaborar el mdk
tendremos 26 = 64
combinaciones.
Note que ahora una casilla, además de
ser adyacente en forma horizontal o vertical, es
adyacente a la casilla que ocupa la misma posición
en el cuadrado cercano horizontal y en el cuadrado
cercano vertical.
Por ejemplo la casilla
10 (001010) es adyacente a las casillas 11(001011),
14(001110), 8(001000), 2(000010) y a las casillas
26(011010) y 42 (101010)
|
|
|
